Oatey is a household name. If you don’t recognize the name, go to your basement, garage, or that catch-all drawer in your kitchen, and I’m sure you’ll find something with their name on it. They have thousands of products to meet the demands of DIYers and professionals alike. With this many products, a wide consumer base, and a commitment to high quality, their website is an important part of their business.
The backstory
Back in 2019, Oatey approached us to refresh their website, but they also wanted to improve the site’s search functionality. We needed to build a search engine to handle approximately 10k queries per day. Searching had to be lightweight and consume minimal system resources since it had to live on the same web server as their catalog API (which we also built), which serves approximately 110k requests per day. The search engine had to 1) provide relevant information in less than 100ms, 2) be able to serve assets in addition to product information, and 3) be scalable to support future Oatey websites. Were we excited to build this? You bet.
Options, so many options
With the requirements out of the way, let’s talk about how we can solve this problem. First, we could use something like Apache Solr or elastic search, but they either require a lot of dev ops work or are overkill, so they were shot down pretty quickly. Second, we could just do simple string finding, but this doesn’t take context into account. For example, if I search “Purple Primer” and product A has the word primer 100 times, but product B has purple once and primer once, which do you rank higher? You’re probably much more interested in product B, but product A has one of your search terms many more times. Even worse, what if I want the terms in the product name to rank higher than the terms in the key features? Oh the conundrum! So how can we determine how close a search phrase is to a product? Enter our final option: Vectors!
So what are vectors? Vectors are these neat mathematical entities that allow you to describe the magnitude and direction of an object. But woah, you may be saying, I get that for things like velocity and acceleration, but words and searching, come on. Bear with me for a moment, and I’ll show you how we incorporated them into our search ranking algorithm.
Did somebody say math?
Let’s go back to our “Purple Primer” search example from earlier. Plotting this search phrase in “word space” gives us Plot 1: Comparison Vector.
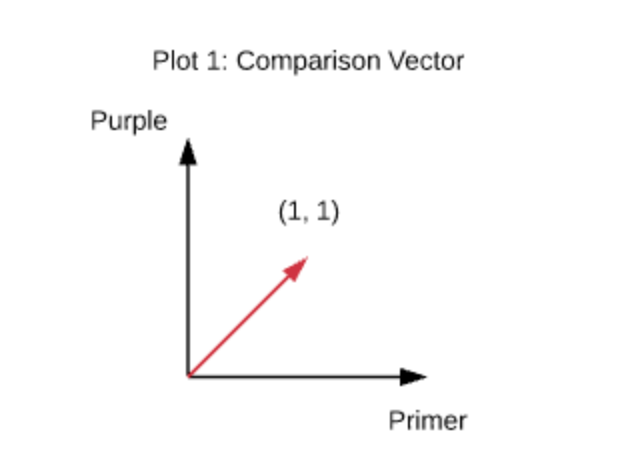
We call this the comparison vector because we will be comparing product data against it. Now, let’s assume we have the products in table 1 to search against.

Table 1
Building our word vector for product A we get (1, 1) for name and (0, 0) for key feature. In detail, primer and purple are each in Name once, and neither term shows up in Key Features. For product B we get (1, 0) and (3, 0). Summing the vectors for product A we get (1, 1) and for product B we get (4, 0). Plotting each of these in word space we get plots 2 and 3 (we scaled them a bit to keep them small).
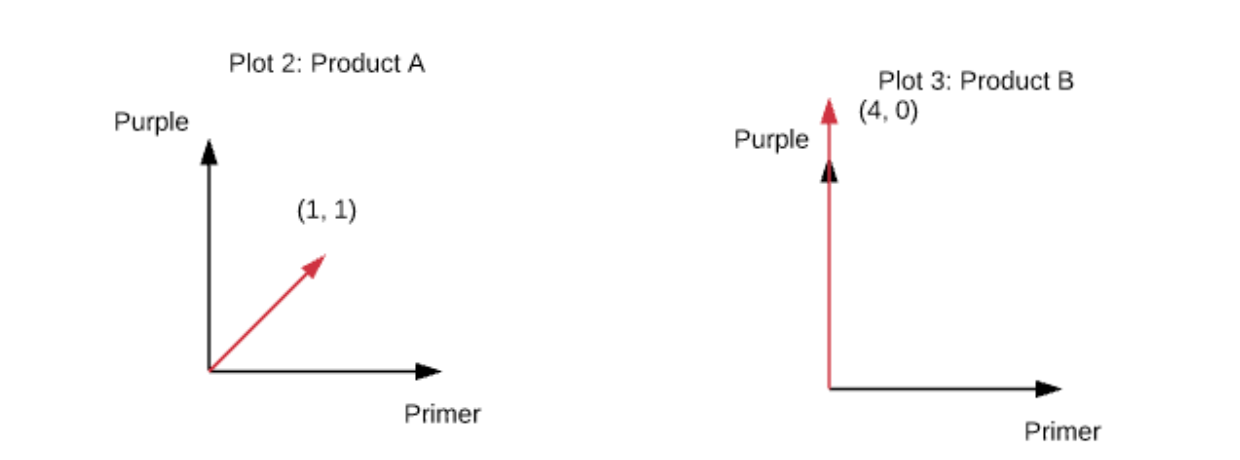
Looking at the graphs, we see that product A is exactly our comparison vector and B is 45 degrees from our comparison vector. Obviously A is what we are searching for, but how do we quantify this? This is where the dot product comes in handy. The vector dot product tells you the angle of separation between two vectors. This is just what we need to determine how close our search phrase is to a product. So for products A and C we have
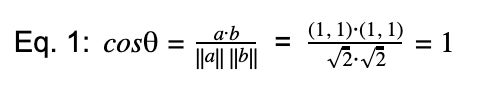
And for product B have
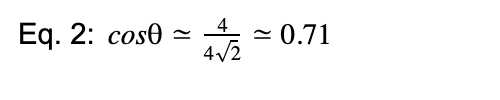
The closer cosθ![]() is to 1, the closer the product is to our search phrase.
is to 1, the closer the product is to our search phrase.
Now we can determine how close our search phrase is to our product, but we should also consider the context in which terms appear. For example, we would like products whose name contains the search terms to rank higher than those whose key feature contains the search terms. If I search for “Purple Primer” I would like to see product A rank higher than product C. How can we do this?
Another feature of vectors is they can be scaled by multiplying them by a scalar (a fancy way of saying a number) and you do not change the direction in which they are pointing. So we can multiply each of our product vectors by a weight to make it longer or “more important” without affecting its dot product. For table 1, we then get
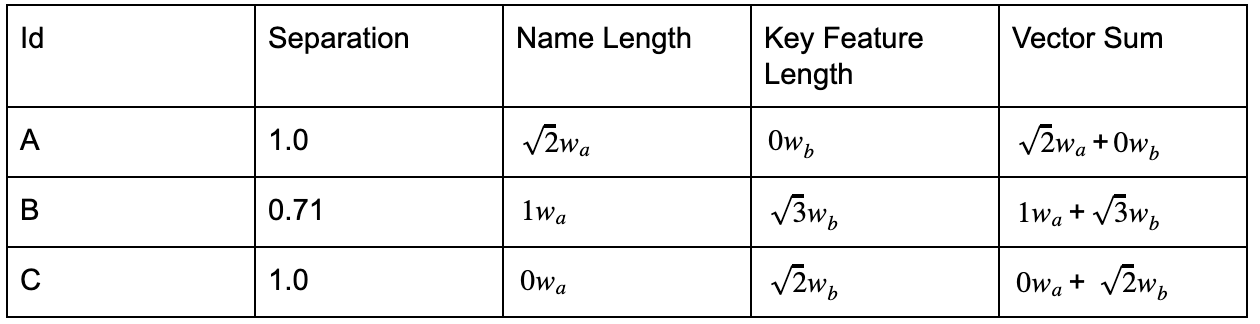
Table 2
Now we are free to choose weights wa![]() and wb
and wb![]() to determine how important a specific attribute is. If we want the product name to be twice as important as its key feature, we set wa
to determine how important a specific attribute is. If we want the product name to be twice as important as its key feature, we set wa![]() to 2 and wb
to 2 and wb![]() to 1. Sorting by separation and then weighted vector length we get
to 1. Sorting by separation and then weighted vector length we get

Table 3
The products are now ranked by how close they are to our search term and also take into account the context in which terms appear. Obviously there are some heuristics and the weights have to be tweaked to meet the requirements of the data, but this method does give quite good results.
The finale
Using vectors we are able to search thousands of products in Oatey’s catalog and provide relevant results very quickly. On average search takes less than 100ms and searches across 15000+ products and 125,000+ attributes. It can serve both products and their associated assets. The method does require some heuristics, but the gain in speed and simplicity greatly outweigh the complexity of other solutions. We only demonstrated a two word search phrase, but it is easily extended to any length search phrase. We just recommend removing duplicate words from the phrase and maybe pruning some other terms that you find not helpful.